CIRCUNFERENCIAS EN EL ORIGEN Y FUERA DEL ORIGEN EN EL PLANO CARTESIANO CON SU ECUACION GENERAL
La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro (recordar que estamos hablando del Plano Cartesiano y es respecto a éste que trabajamos).
Determinación de una circunferencia
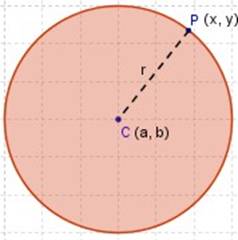
Una circunferencia queda determinada cuando conocemos:
Tres puntos de la misma, equidistantes del centro.
El centro y el radio.
El centro y un punto en ella.
El centro y una recta tangente a la circunferencia.
También podemos decir que la circunferencia es la línea formada por todos los puntos que están a la misma distancia de otro punto, llamado centro .
Esta propiedad es la clave para hallar la expresión analítica de una circunferencia (laecuación de la circunferencia ).
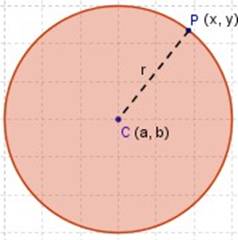
Entonces, entrando en el terreno de la Geometría Analítica , (dentro del Plano Cartesiano ) diremos que ─para cualquier punto, P (x, y) , de una circunferencia cuyo centro es el punto C (a, b) y con radio r ─, la ecuación ordinaria es
(x ─ a) 2 + (y ─ b) 2 = r 2
¿Qué significa esto?
En el contexto de la Geometría Analítica significa que una circunferencia graficada con un centro definido (coordenadas) en el Plano Cartesiano y con radio conocido la podemos “ver” como gráfico y también la podemos “transformar” o expresar como una ecuación matemática.
Así la vemos
|
|
|
| Así podemos expresarla |
Donde:
(d) Distancia CP = r
y
Fórmula que elevada al cuadrado nos da
(x ─ a) 2 + (y ─ b) 2 = r 2
También se usa como
(x ─ h) 2 + (y ─ k) 2 = r 2
|
Recordar siempre que en esta fórmula la x y la y serán las coordenadas de cualquier punto (P) sobre la circunferencia, equidistante del centro un radio (r) . Y que la a y la b(o la h y la k , según se use) corresponderán a las coordenadas del centro de la circunferencia C(a, b) .
Nota importante:
Los ejercicios sobre esta materia pueden hacerse en uno u otro sentido.
Es decir, si nos dan la ecuación de una circunferencia , a partir de ella podemos encontrar las coordenadas de su centro y el valor de su radio para graficarla o dibujarla.
Y si nos dan las coordenadas del centro de una circunferencia y el radio o datos para encontrarlo, podemos llegar a la ecuación de la misma circunferencia.
Cuadrado del binomio
Aquí haremos una pausa para recordar el cuadrado del binomio ya que es muy importante para lo que sigue:
El binomio al cuadrado de la forma (a ─ b) 2 podemos desarrollarlo como (a ─ b) (a ─ b) o convertirlo en un trinomio de la forma a 2 ─ 2ab + b 2 .
|
Sigamos nuestro razonamiento sobre la ecuación (x ─ a) 2 + (y ─ b) 2 = r 2 (que en forma matemática representa una circunferencia).
De la ecuación ordinaria a la ecuación general
Si en esta ecuación ordinaria ─cuyo primer miembro (lado izquierdo) está formado por la suma de dos cuadrados de binomio─, eliminamos los paréntesis desarrollando dichos binomios, pasamos todos los términos al primer miembro y la igualamos a cero, tendremos:
x 2 ─ 2ax + a 2 + y 2 ─ 2by + b 2 ─ r 2 = 0 ecuación que ordenada sería
x 2 + y 2 ─ 2ax ─ 2by + a 2 + b 2 ─ r 2 = 0
Si para tener una ecuación más sintetizada hacemos las siguientes asignaciones:
─ 2a = D,
─ 2b = E,
a 2 + b 2 ─ r 2 = F
la ecuación quedaría expresada de la forma:
x 2 + y 2 + Dx + Ey + F = 0 conocida como Ecuación General de la Circunferencia,la cual debe cumplir las siguientes condiciones para serlo:
No existe término en xy
Los coeficientes de x 2 e y 2 son iguales.
Si D = ─ 2a entonces 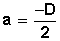
Si E = ─ 2b entonces 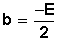
Si F = a 2 + b 2 ─ r 2 entonces 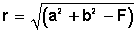
Además, otra condición necesaria para que una ecuación dada represente una circunferencia es que:
a 2 + b 2 ─ F > 0 (a 2 + b 2 ─ F debe ser mayor que cero)
Nota:
Para simplificar la ecuación general de la circunferencia (x 2 + y 2 ─ 2ax ─ 2by + a 2 + b 2 ─ r 2 = 0) algunos textos o docentes utilizan otra convención y hacen:
─ 2a = A,
─ 2b = B,
a 2 + b 2 ─ r 2 = C para tener finalmente
x 2 + y 2 + Ax + By + C = 0 que es lo mismo que x 2 + y 2 + Dx + Ey + F = 0
A modo de recapitulación
Si conocemos las coordenadas del centro y el radio de una circunferencia, podemos construir su ecuacion ordinaria, y si operamos los binomios cuadrados que la conforman, obtenemos la forma general de la ecuación de la circunferencia.
Ecuación reducida de la circunferencia
Volviendo a nuestra ecuación ordinaria (x ─ a) 2 + (y ─ b) 2 = r 2 , debemos consignar que si el centro de la circunferencia coincide con el origen de coordenadas (0, 0) la ecuación queda reducida a:
( x ─ a) 2 + (y ─ b) 2 = r 2
(x ─ 0) 2 + (y ─ 0) 2 = r 2
x 2 + y 2 = r 2
Ir a:
Sobre esta materia, actividades en Internet:
1.- Cálcula en esta actividad el centro y el radio de una circunferencia de ecuación en forma general .